Selecting Large Language Model to Fine-tune via Rectified Scaling Law

Abstract

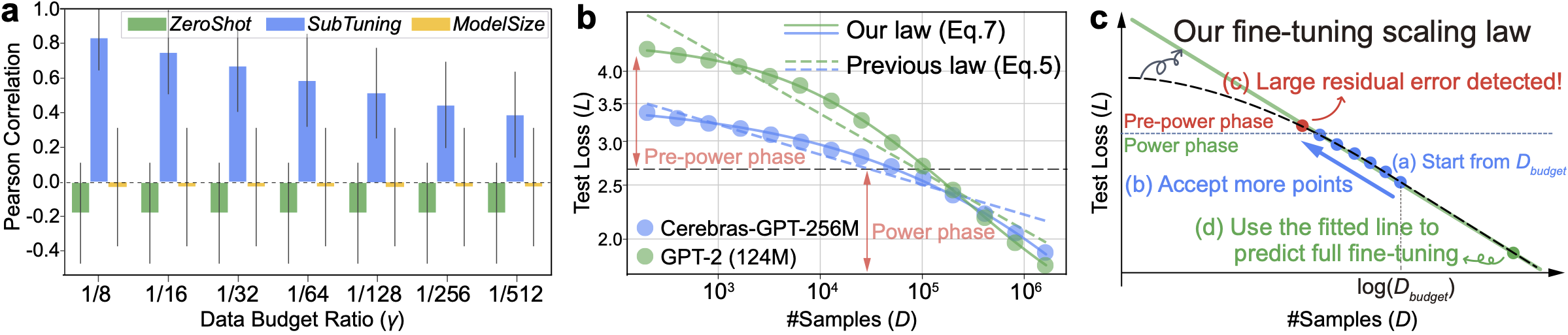
The ever-growing ecosystem of LLMs has posed a challenge in selecting the most appropriate pre-trained model to fine-tune amidst a sea of options. Given constrained resources, fine-tuning all models and making selections afterward is unrealistic. In this work, we formulate this resource-constrained selection task into predicting fine-tuning performance and illustrate its natural connection with Scaling Law. Unlike pre-training, we find that the fine-tuning scaling curve includes not just the well-known "power phase" but also the previously unobserved "pre-power phase". We also explain why existing Scaling Law fails to capture this phase transition phenomenon both theoretically and empirically. To address this, we introduce the concept of "pre-learned data size" into our Rectified Scaling Law, which overcomes theoretical limitations and fits experimental results much better. By leveraging our law, we propose a novel LLM selection algorithm that selects the near-optimal model with hundreds of times less resource consumption, while other methods may provide negatively correlated selection.

TL;DR

We first formulated the problem of LLM selection and rectified the Scaling Law for fine-tuning senarios. Based on this rectified scaling law, we designed an effective method to address model selection problem.

Scaling Law Fails?

Figure a demonstrates the Pearson correlation between the true full-fine-tuning performance and the predicted performance of 3 heuristic methods, given different resource constraints denoted by γ. These baseline methods cannot predict performance well especially under demanding constraints (small $ γ $), and could even provide negatively correlated predictions.

Figure b displays the phase transition phenomenon observed in the scaling of fine-tuning loss $L$ with training sample size $D$. In addition to the widely studied power phase where $(L,D)$ are linearly correlated under the log-log scale, we discover the pre-power phase when $D$ is small. Previous laws fail to fit both phases, while our proposed law fits quite well.

Figure c summarizes our LLM selection algorithm that extrapolates full-fine-tuning performance based on the new law.

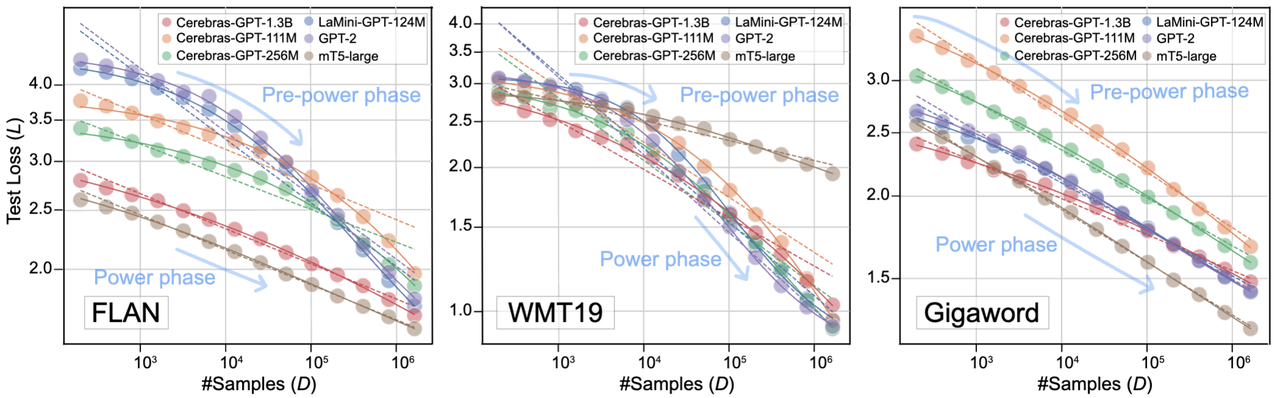
We chose 3 datasets and plotted the phase transition from pre-power phase to power phase, and the fitness of different Scaling Laws. The x and y axes are fine-tuning dataset size D and test loss L in log scale. Each subfigure corresponds to a dataset. Solid lines are the fitting results of our law, and dash lines are the fitting results of vanilla law.

Algorithm and Findings

The vanilla scaling law is:

$$ \mathcal{L}(D) = \left(\frac{B}{D^\beta}+E\right)^\alpha. $$

We define the rectified scaling law with dataset size $D$ for fine-tuning as:

$$ \mathcal{L}(D) = \left(\frac{B}{D_l+D^\beta}+E\right)^\alpha. $$

The algorithm is as follows:

Results

We compared the proposed model selection method (AtS) with 3 intuitive methods. Results show that our method excels under different training budget ratios.

This table summarizes all the models we used in experiments. The Arch. is short for model architecture, De-only, En-De and Moe stands for Decoder-only, Encoder-Decoder and Mixture of Experts respectively. The last few columns summarize the configuration of different language models, including number of parameters, number of layers, dimension of hidden states, number of attention heads, dimension of feed-forward layers, and dimension of key/value head.

BibTeX

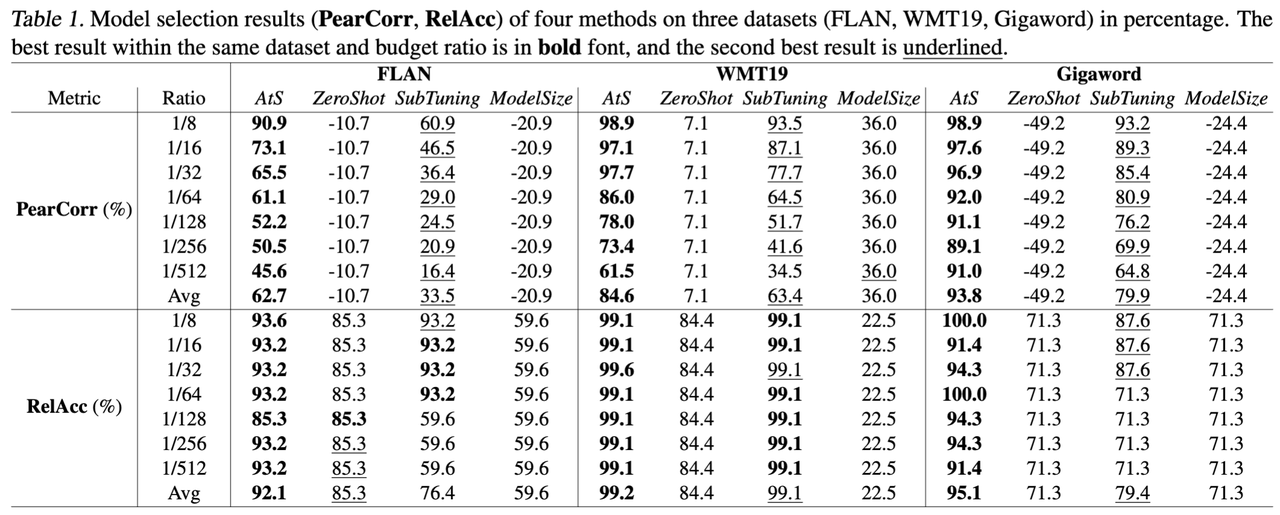
@article{lin2024selecting,
      author    = {Haowei, Lin and Baizhou, Huang and Haotian, Ye and Qinyu, Chen and Zihao, Wang and Sujian, Li and Jianzhu, Ma and Xiaojun, Wan and James, Zou and Yitao, Liang},
      title     = {Selecting Large Language Model to Fine-tune via Rectified Scaling Law},
      journal   = {ICML},
      year      = {2024},
    }